Revisiting Throughput

This is a note about throughput and latency from the perspective of Software and Hardware.

Overview

In the scenario of analyzing the performance of a DNN model, throughput and latency are two fundamental metrics. While these terms are often understood at a high level, when considering them from both hardware and software perspectives at the same time, there are important factors that are often overlooked.

Basic Concepts about Throughput and Latency

Throughput is defined as the amount of data that can be processed/completed in a given time period. We can report it as :

$$ \begin{align} \text{Throughput} &= \frac{\text{Number of operations}}{\text{seconds}} \tag{1} \\ \end{align} $$

Applications require high throughput when a system involves large-scale data processing, where maximizing the number of processed units per second is critical. For example, real-time video processing, security and surveillance, medical diagnosis, and drug discovery all benefit from high throughput.

Latency is the time taken to complete a single operation. We can report it as :

$$ \begin{align} \text{Latency} &= \text{Time}_{\text{output generated}} - \text{Time}_{\text{input arrives to a system}} \tag{2}\\ \end{align} $$

In general, real-time interative applications, such as AR, autonomous navigation and robotics, require low latency to ensure a smooth user experience.

A Deeper Look at Throughput

Factors Affecting Throughput

In model inference perspective, throughput is considered as inference per second. Firstly, we can break it down into two components:

$$ \begin{align} \frac{\text{inferences}}{\text{seconds}} &= \frac{\text{operations}}{\text{seconds}} \times \frac{1}{\frac{\text{operations}}{\text{inferences}}} \tag{3} \\ \end{align} $$

The denominator of second term is dictated by only DNN models , because it is defined as how many operations are required to complete a single inference.
For the first term, we can further break it down:

$$ \begin{align} \frac{\text{operations}}{\text{seconds}} = \left( \frac{1}{\frac{\text{cycles}}{\text{operations}}} \times \frac{\text{cycles}}{\text{second}} \right) \times \text{number of PEs} \times \text{utilization of PEs} \tag{4} \end{align} $$

Here, we consider a system comprised of multiple processing elements (PEs), where PE means a simple or primitive core that performs a single MAC operation.

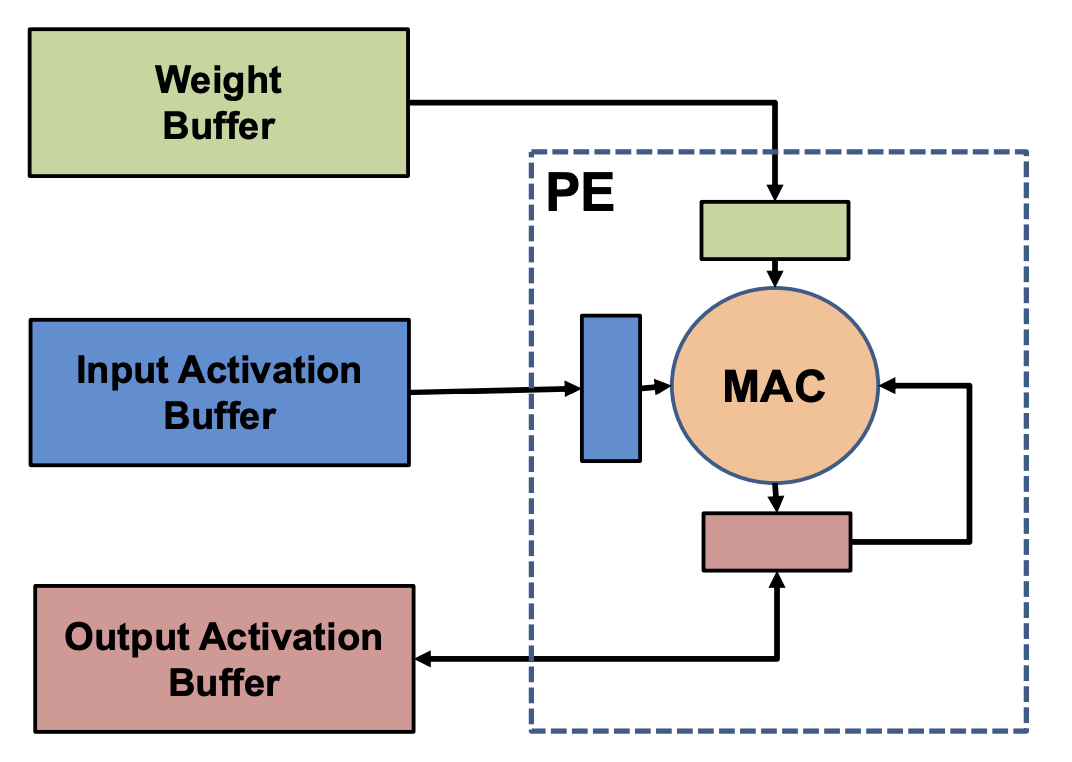
Let’s take a closer look at each term:

1. $\frac{1}{\frac{\text{cycles}}{operation}}$ is IPC (Instructions per Cycle), which is the number of operations that can be completed in a single cycle.
2. $\frac{\text{cycles}}{\text{second}}$ is the clock rate of the system.
   The combination of these two terms is the peak throughput of the system, which is the maximum number of operations that can be completed in a second.
3. $\text{number of PEs}$ means the amount of parallelism in the system.
4. $\text{utilization of PEs}$ is the fraction of time that the PEs are busy performing operations.
   This term is determined by DNN model(i.e. memory-bound or not).

Back to equation (3), we can say that the first term is dictated by DNN hardware and DNN models, while the second term is dictated by the DNN model.

Increase Throughput

If we want to increase throughput from a hardware perspective, we can consider the following:

1. Increase $\frac{\text{cycle}}{\text{second}}$ $\rightarrow$ higher clock rate $\rightarrow$ reducing critical path.

   • Affected by design of the MAC.

2. Increase number of PEs $\rightarrow$ multiple MACs perform in parallel.

   • If area cost of the system is fixed
     • Increasing the area density of the PEs.
     • Trading off on-chip storage area for more PEs.
   • Increasing the density of PEs
     • Reducing the logic associated with delivering operands to a MAC.
       • Multiple MACs share control logic.

3. $\text{utilization of PEs} = \frac{\text{number of active PEs}}{\text{number of PEs}} \times \text{utilization of active PEs}$
   First term means ability to distribute the workload to PEs. (在做事的PE/所有PE)
   Second term means how efficiently those active PEs are processing the workload. (做有用的事情的PE)

Effectual and Ineffectual Opertaions

If we consider effectual and ineffectual operations, we can further break down the first term of equation (4) as follows:

$$ \begin{align} \frac{\text{operations}}{\text{cycle}} = \frac{\text{EO} + \text{UIO}}{\text{cycle}} \times \frac{\text{EO}}{\text{EO} + \text{UIO}} \times \frac{1}{\frac{\text{EO}}{\text{operations}}} \tag{5} \end{align} $$

where $\textbf{EO}$ is effectual operations and $\textbf{UIO}$ is unexploited ineffectual operations(e.g. MAC accumulates anything multiplied by zero $\rightarrow$ $\color{red}{\text{sparsity}}$).
In equation (5), the first term is a constant for a given hardware accelerator design, the second term is the ability of the hardware to exploit the ineffectual operations(硬體發覺無效計算的能力), and the last term is related to amount of sparsity and depends on the DNN model.

Reducing Precision (e.g. Quantization)

Lowering precision of computation, such as through quantization is a common optimization technique. Lower precision means fewer bits to process per operation, which reduces the bandwidth requirements. This allows for higher utilization of PEs, ultimately leading to increased throughput(i.e. more operations per second).
However, supporting multiple levels of precision require additional hardware, which may increase the critical path and reduces the area density of PEs. This results in a decrease in overall throughput.

Factors that Affect Inference per Second

Based on the above discussion, we can summarize the factors that affect inference per second as this table:

Factor	Hardware	DNN Models	Input Data
Operations per inference		✓
Operations per cycle	✓
Cycles per second	✓
Number of PEs	✓
Number of active PEs	✓	✓
Utilization of active PEs	✓	✓
Effectual operations out of (total) operations		✓	✓
Effectual operations plus unexploited ineffectual operations per cycle	✓

Reference

1. Course slides of Edge AI, NYCU.