Backpropagation 反向傳播

學PyTorch不如自己刻一次Backpropagation。

Opening

本篇文章是建立在對Gradient Descent、Neural Network架構有基礎了解的前提下，介紹如何透過Backpropagation來更新神經網路的參數，並且使用NumPy手刻出Backpropagation的過程。

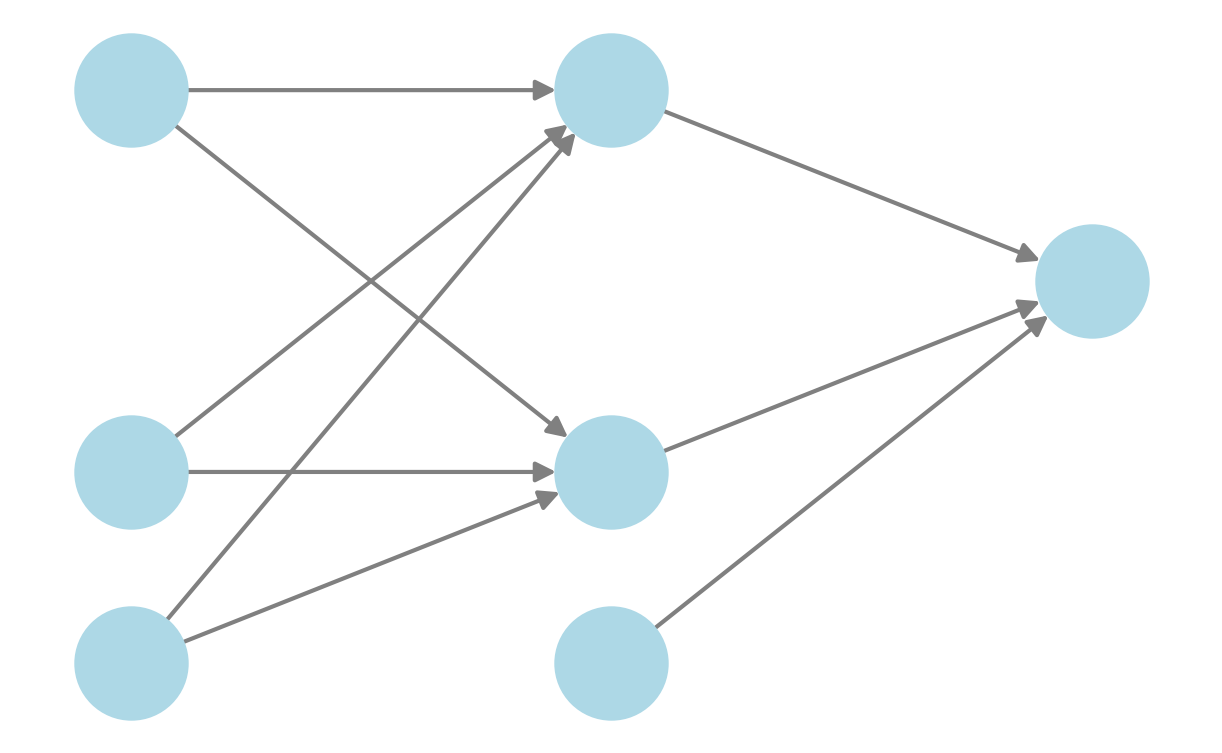
Forward 向前傳播

首先，先來看神經網路的基本架構：

這是一個簡易的神經網路，輸入、隱藏層皆有兩個Neurons加上一個Bias，輸出則有一個Neurons。對於某Neuron $X_i$，向前傳播過程可以寫成：

$$ \begin{aligned} Z^{(1)}_j &= \sum_{i=1}^{D} W^{(1)}_{ij}X_i + B^{(1)}_j \\ A^{(1)}_j &= h(Z^{(1)}_j) \\ Z^{(2)}_k &= \sum_{j=1}^{M} W^{(2)}_{jk}A^{(1)}_j + B^{(2)}_k \\ A^{(2)}_k &= Z^{(2)}_k \\ \text{E}(W,B) &= \frac{1}{2 } \sum_{k=1}^{K} (A^{(2)}_k - Y_k)^2 \end{aligned} $$

這裡的$h$表示隱藏層的激活函數（Activation Function），這裡因為以Regression為例，所以輸出層的激活函數為Identity Function。$\text{E}$表示Loss Function，這裡以Mean Squared Error為例。 若僅考慮Variables/Activations的Dependency，可以寫成：

$$ \begin{aligned} X_i \rightarrow W^{(1)}_{ij} \rightarrow Z^{(1)}_j \rightarrow A^{(1)}_j \rightarrow W^{(2)}_{jk} \rightarrow Z^{(2)}_k \rightarrow A^{(2)}_k \leftrightarrow Y_k \rightarrow \text{E} \end{aligned} $$

Backward 反向傳播

接著，我們要來更新$W^{(2)}$的參數，我們的目標是計算$\frac{\partial E}{\partial W^{(2)}_{jk}}$，但這個東西很難直接算出來，因此我們考慮使用Chain Rule，透過上式的Dependency關係將其拆成 :

$$ \begin{aligned} \frac{\partial E}{\partial W^{(2)}_{jk}} &= \frac{\partial E}{\partial Z^{(2)}_k} \cdot \frac{\partial Z^{(2)}_k}{\partial W^{(2)}_{jk}} \\ \end{aligned} $$

透過一些簡單的偏微分計算，我們得到：

$$ \begin{aligned} \frac{\partial E}{\partial Z^{(2)}_k} &= A^{(2)}_k - Y_k = \delta_{k} \\ \frac{\partial Z^{(2)}_k}{\partial W^{(2)}_{jk}} &= A^{(1)}_j \end{aligned} $$

接著再次使用Chain Rule，分解$\frac{\partial E}{\partial W^{(1)}_{ij}}$：

$$ \begin{aligned} \frac{\partial E}{\partial W^{(1)}_{ij}} &= \sum_{k=1}^{K} \left( \frac{\partial E}{\partial Z^{(2)}_k} \cdot \frac{\partial Z^{(2)}_k}{\partial Z^{(1)}_j} \cdot \frac{\partial Z^{(1)}_j}{\partial W^{(1)}_{ij}} \right) \\ \end{aligned} $$

再複習一次大一微積分：

$$ \begin{aligned} \frac{\partial E}{\partial Z^{(2)}_k} &= \delta_{k} \\ \frac{\partial Z^{(2)}_k}{\partial Z^{(1)}_j} &= W^{(2)}_{jk} \cdot h^{'}(Z^{(1)}_j) \\ \frac{\partial Z^{(1)}_j}{\partial W^{(1)}_{ij}} &= X_i \end{aligned} $$

其中，我們定義第一層的誤差信號 $\delta_j$ 為：

$$ \begin{aligned} \delta_j &= \frac{\partial E}{\partial Z^{(1)}_j} = \sum_{k=1}^{K} W^{(2)}_{jk} \delta_k h'(Z^{(1)}_j) \end{aligned} $$

將上述幾式整理，我們可以得到：

$$ \begin{aligned} \frac{\partial E}{\partial W^{(2)}_{jk}} &= \delta_{k} \cdot A^{(1)}_j \\ \frac{\partial E}{\partial W^{(1)}_{ij}} &= \delta_{j} \cdot X_i \end{aligned} $$

對於Bias的Gradient，其實就是：

$$ \begin{aligned} \frac{\partial E}{\partial B^{(2)}_{k}} &= \delta_{k} \\ \frac{\partial E}{\partial B^{(1)}_{j}} &= \delta_{j} \end{aligned} $$

如此一來我們就算完最複雜的部分了，可以進入實作了！

Implementation

在開始實作前，我們先釐清各個矩陣的維度：

符號	說明	維度
$X$	輸入矩陣	(m, n_input)
$W^{(1)}$	第一層的權重矩陣	(n_input, n_hidden)
$B^{(1)}$	第一層的偏差矩陣	(1, n_hidden)
$Z^{(1)}$	第一層的線性組合	(m, n_hidden)
$A^{(1)}$	第一層的激活函數結果	(m, n_hidden)
$W^{(2)}$	第二層的權重矩陣	(n_hidden, n_output)
$B^{(2)}$	第二層的偏差矩陣	(1, n_output)
$Z^{(2)}$	第二層的線性組合	(m, n_output)
$A^{(2)}$	第二層的激活函數結果	(m, n_output)

其中，m為Batch Size，n_input為輸入的特徵數，n_hidden為隱藏層的Neuron數，n_output為輸出的Neuron數。

Forward

def forward(self, x):
    """
    Parameters:
        x (numpy.ndarray): Input matrix of shape (batch_size, n_input).

    Returns:
        numpy.ndarray: Output matrix of shape (batch_size, n_output).
    """
    self.z1 = np.matmul(x, self.w1) + self.b1
    self.a1 = self.ReLU(self.z1)
    self.z2 = np.matmul(self.a1, self.w2) + self.b2
    self.a2 = self.z2
    return self.a2

在這裡選用ReLU作為隱藏層的Activation Function。

Backward

def backward(self, X, y, pred, lr):
    """
    Parameters:
        X (numpy.ndarray): Input matrix of shape (batch_size, n_input).
        y (numpy.ndarray): Target matrix of shape (batch_size, n_output).
        pred (numpy.ndarray): Output matrix of shape (batch_size, n_output).
        lr (float): Learning rate.
    """
    # STEP 1
    batch_size = X.shape[0]
    delta_output = 2 * (pred - y) / batch_size

    # STEP 2
    dw2 = np.matmul(self.a1.T, delta_output)
    db2 = np.sum(delta_output, axis=0, keepdims=True)

    # STEP 3
    delta_hidden = np.matmul(delta_output, self.w2.T) * self.ReLU_derivative(self.z1)

    # STEP 4
    dw1 = np.matmul(X.T, delta_hidden)
    db1 = np.sum(delta_hidden, axis=0, keepdims=True)

    # UPDATE
    self.w1 -= lr * dw1
    self.b1 -= lr * db1
    self.w2 -= lr * dw2
    self.b2 -= lr * db2

這裡的ReLU_derivative是ReLU的導函數（也可以換成其他Activation Function，但記得要differentiable）。
$ \delta_k \text{加了} \frac{2}{\text{batch_size}}$ 常數是因為真正MSE函式應為 np.mean((A - Y) ** 2)，這個mean是指將$\textbf{所有資料}$的Square Error取平均，而上面的MSE公式則是為了讓$\textbf{單一資料}$Gradient計算時會比較漂亮，所以乘了一個$\frac{1}{2}$。
當初在寫Backward時一直不懂矩陣到底要怎麼乘，但後來發現只要想清楚上面的公式，再對照好矩陣維度就可以了！

Training

再來來寫一個簡單的Training Function：

def train(self, X, y, epochs=1000, lr=0.01, verbose=10):
   """
   Parameters:
       X (numpy.ndarray): Input matrix of shape (batch_size, n_input).
       y (numpy.ndarray): Target matrix of shape (batch_size, n_output).
       epochs (int): Number of epochs.
       lr (float): Learning rate.
       verbose (int): Frequency of printing the loss
   """
   for epoch in range(epochs):
       pred = self.forward(X)
       loss = self.MSE(y, pred)
       self.backward(X, y, pred, lr)
       if epoch % verbose == 0:
           print(f"Epoch {epoch}, Loss: {loss:.6f}")

Conclusion

這裡我以Regression為例，但實際上只要將Loss Function、Activation Function換掉，就可以應用在其他任務上。以下是一些常見的任務：

Tasks	輸出層 Activation Function	Loss Function
回歸（Regression）	Identity Function	Mean Squared Error
二元分類（Binary Classification）	Sigmoid	Binary Cross-Entropy
多類分類（Multi-Class Classification）	Softmax	Categorical Cross-Entropy

再做一些微分時小小的修改就可以了。但我認為重點在於理解Backpropagation中使用Chain Rule的技巧，還有計算Partial Derivative的一些細節。