WQS 二分搜

一篇WQS二分搜的筆記，希望能讓自己不要這麼快忘記的個優化技巧。

Introduction

WQS 二分搜又稱Aliens優化，是一個可以將二維的DP問題轉化成一個維度的優化技巧
複雜度可以從$O(N^2)$下降到$O(NlogC)$，但題目本身需要一些特性。
已知某函數$f(x)$為concave function，且我們有某種演算法可以在線性時間內求出$f(x) - px$的最大值及最大值
發生的位置($x_0$)。
接下來，我們畫出$p=0 - 5$的Cases :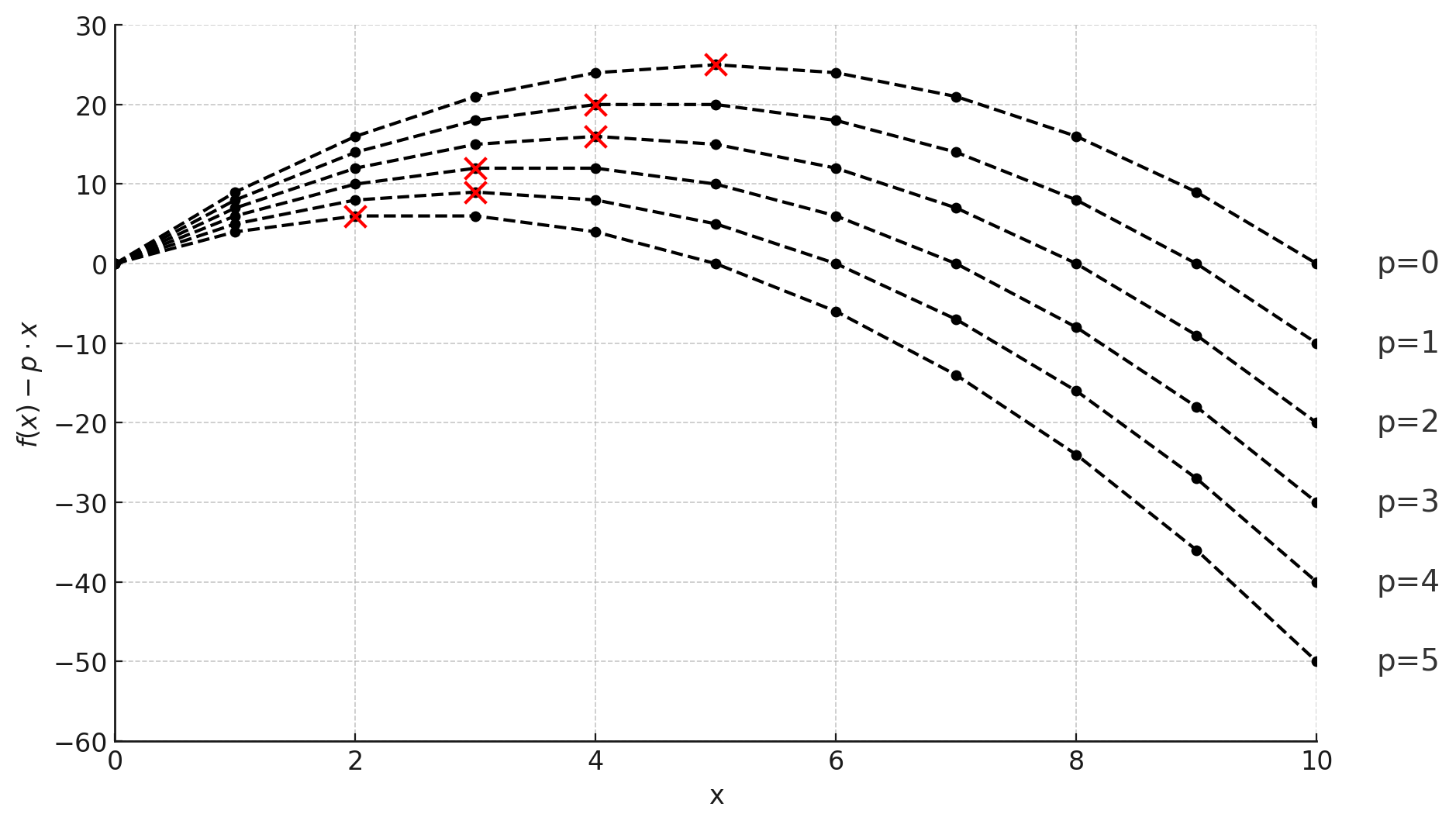

可以發現，$x_0$隨著$p$上升逐漸下降！
因此若我們希望找到$f(x)$的最大值且$x<=k$，我們可以對$p$做二分搜，找到最近的$p$使得$f(x) - px$的$x_0$$\le k$，最後答案就會是演算法的輸出$+ pk$。

Informal Proof

至於為什麼當p越大，極值發生位置會越來越前面，簡單的證明如下：
當$f(x)$極值發生時的必要條件是$\nabla f(x) = 0$
$\nabla (f(x) - px) = \nabla f(x) - \nabla px = \nabla f(x) - p = 0$
已知$f(x)$是concave，因此 $\nabla f(x)$ 遞減
因此當$p \uparrow$，$x$必須越來越小。
然而，WQS真正困難的部分其實是證明$f(x)$是concave的，很多時候看到題目都會靠直覺猜它是concave，然後直接使用此性質（就像猜某個greedy方式會是最佳解）。

Intuition

我覺得WQS二分搜有一個很好的intuition：
$f(x)$是某件事做了$x$次後得到的值，$p$就可以當作每做一次所需的成本，當成本($p$)越大，我們就不能做太多次操作（若我們的目標是maximize $f(x)$）。
因此！理所當然當$p$越大，$x_0$就會越小。

Application

直接來看一題很經典的WQS二分的題目AI-666 賺多少：
題目敘述：給定$n$天股票價格，求只能交易$k$次的情況下最多能賺多少錢？（假設最多同時只能持有一張股票）
這題有一個很簡單的dp解：
$dp0[i][j]$表示在第$i$天，交易了$j$次且當下沒有股票的最佳解
$dp1[i][j]$表示在第$i$天，交易了$j$次且當下持有股票的最佳解
轉移式：
$dp0[i][j] = max(dp0[i-1][j], dp1[i-1][j-1] + a[i])$
$dp1[i][j] = max(dp1[i-1][j], dp0[i-1][j] - a[i])$
最後答案就是$dp0[n][k]$。
但很明顯，此做法的時間、空間複雜度為$O(n^2)$。
嘗試將問題轉換成「不限制交易次數」，我們可以發現轉移式就會變成：
$dp0[i] = max(dp0[i-1], dp1[i-1] + a[i])$
$dp1[i] = max(dp1[i-1], dp0[i-1] - a[i])$
其中，$dp0[i]$表示在第$i$天，當下沒有股票的最佳解，$dp1[i]$表示在第$i$天，當下持有股票的最佳解。
接著，我們嘗試將每次交易都增加一個$p$元的手續費，此時轉移式變成：
$dp0[i] = max(dp0[i-1], dp1[i-1] + a[i])$
$dp1[i] = max(dp1[i-1], dp0[i-1] - a[i] - p)$
我們可以在$O(n)$的時間解決這個「有手續費且沒有交易次數限制」的問題。
最後，我們可以對$p$做二分搜找到某個$p$，使得發生最大值時的交易次數$\leq k$
最終答案就會是此演算法的輸出$+ pk$。

#include <bits/stdc++.h>
#define int long long
#define ll long long
#define pb push_back
#define sz(x) (x).size()
#define all(x) (x).begin(), (x).end()
#define fastio cin.tie(0); ios_base::sync_with_stdio(false);
using namespace std;
const int maxn = 2e6+5;
const int mod = 1e9+7; // 998244353;
const ll inf = 1ll << 61;
typedef pair<int,int> P;
int n, k;
int a[maxn];
P dp0[maxn], dp1[maxn];

void init(){
    dp0[0] = P(0, 0);
    dp1[0] = P(-inf, 0);
}

P cal(int p){
    init();
    P res = {0, inf};
    for(int i=1;i<=n;i++){
        // 沒股票
        if(dp0[i-1] > P(dp1[i-1].first + a[i] - p, dp1[i-1].second - 1))
            dp0[i] = dp0[i-1];
        else
            dp0[i] = P(dp1[i-1].first + a[i] - p, dp1[i-1].second - 1);
        // 有股票
        if(dp1[i-1] > P(dp0[i-1].first - a[i], dp0[i-1].second))
            dp1[i] = dp1[i-1];
        else
            dp1[i] = P(dp0[i-1].first - a[i], dp0[i-1].second);
        res = max(res, dp0[i]);
    }
    return res;
}

void solve(){
    cin >> n >> k;
    for(int i=1;i<=n;i++)
        cin >> a[i];
    int l = 0, r = 5e4;
    P res = cal(0);
    int pp;
    if(-res.second <= k){
        cout << res.first;
        return;
    }
    while(l <= r){
        int mid = (l + r) / 2;
        res = cal(mid);
        if(-res.second > k){
            pp = mid;
            l = mid + 1;
        } 
        else{
            r = mid - 1;
        }
    }
    cout << cal(pp+1).first + (pp+1) * k;
}

signed main(){fastio
    int T = 1;
    //cin >> T;
    while(T--){
        solve();
    }
}

在TIOJ上要稍微壓一點常數（e.g. 二分搜範圍）

WQA二分搜的過程其實有不少細節，請未來的我自行體會。
但就結論而言，一個簡單且可以避免錯誤的方法是「找最大的$p$使得最後的交易次數不滿足題目限制」
最後我們所需$p$就會是$p+1$(如果是離散的話)。

Related Problems

美食博覽會 (k 值加大版)
Subarray Squares
Tree I
E2. Guard Duty (medium)
F. New Year and Handle Change
E. Gosha is hunting